AR, MA : 자기 회귀 모델과 이동 평균 모델

자기 회귀 모델 (AR, Autoregressive Model)

자기 회귀 모델은 변수의 과거 값의 선형 조합을 이용하여 현재 변수의 값을 예측한다.

즉, 과거의 자기 자신 값으로 현재 항을 찾는 모델이다.

 

 

<차수가 p인 AR(p) 자기 회귀 모형: AR(p) >

$$ y_{t} = c + \phi_{1}y_{t-1} + \phi_{2}y_{t-2} + \dots + \phi_{p}y_{t-p} + \varepsilon_{t} $$

$\varepsilon_{t}$ 는 백색 잡음(i.i.d를 따름)을 의미한다

 

다양한 AR(1) 모델

$$ y_t = c + \phi_1 y_{t-1} + \epsilon_t $$

 

⋁ $\phi_1 = 0, \ c=0$ 일 때, $y_t$ : 백색 잡음

⋁ $\phi_1 = 1,\ c = 0$ 일 때, $y_t$ : 확률 보행 모델

⋁ $\phi_1 = 1,\ c \ne 0$ 일 때, $y_t$ : 표류가 있는 확률 보행 모델

⋁ $\phi_1 < 0$ 일 때, $y_t$ : 평균값을 중심으로 진동하는 경향

 

AR(1) 모델의 경우,

$−1<\phi_1<1$ 의 조건을 만족해야 정상성을 띄는 모델이라고 말할 수 있다.

 

그렇다면 왜 정상성을 띄는 조건이 위와 같을까?

아래와 같은 유도로 파악할 수 있다.

그러므로,

확률 보행 모델은 정상성을 띄지 않는 모델이다.

 

좀 더 자세히 살펴보면,

확률 보행 모델은 시간이 지남에 따라 분산이 증가하여 변수의 분포가 시간에 따라 변하기 때문이다.

$$ Var(y_t) = Var(\epsilon_1 + \cdots + \epsilon_t) = Var(\epsilon_1) + \cdots + Var(\epsilon_t) = t\sigma^2 $$

$$ Var(\sum_{t=1}^T \epsilon_t) = \sum_{t=1}^T Var (\epsilon_t) $$

위와 같이 분산 값이 t값에 의존하게 되어 시간이 지남에 따라 분산이 커지게 되는 것을 알 수 있다.

 

정상성이 정의되려면, 분산이 상수여야 하므로 확률 보행 모델은 정상성을 띄지 않는 것을 확인할 수 있다. 

따라서 확률 보행 모델은 확률론적 추세(Stochastic trend)가 존재하는 가장 단순한 모델이다.

 

이동 평균 모델 (MA, Moving Average Model)

과거와 현재 자신의 오차 관계를 정의하는 모델,

이는 이전 항의 오차로 현재 항의 상태를 주론 하겠다는 의미와 같다

변화하는 추세를 반영하겠다는 의미로도 볼 수 있다.(과거의 보고자 하는 변수 밖에서의 추세는 AR이 잡아낼 수 없음!)

 

과거의 충격이 현재에 영향을 주는 경우 사용한다.

$$ y_t = c + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q},\ \epsilon_t \sim N(0,\sigma^2) $$

 

< MA가 정상성을 만족하는 이유 >

사실 iid를 따르는 오차를 이용한 식을 가진 모델이기 때문에 평균과 분산이 일정할 수밖에 없다.

그러므로 항상 정상성을 가질 수 있는 것..!

 

아래 MA(1) 모형에 대한 간단한 증명을 첨부했다.

 

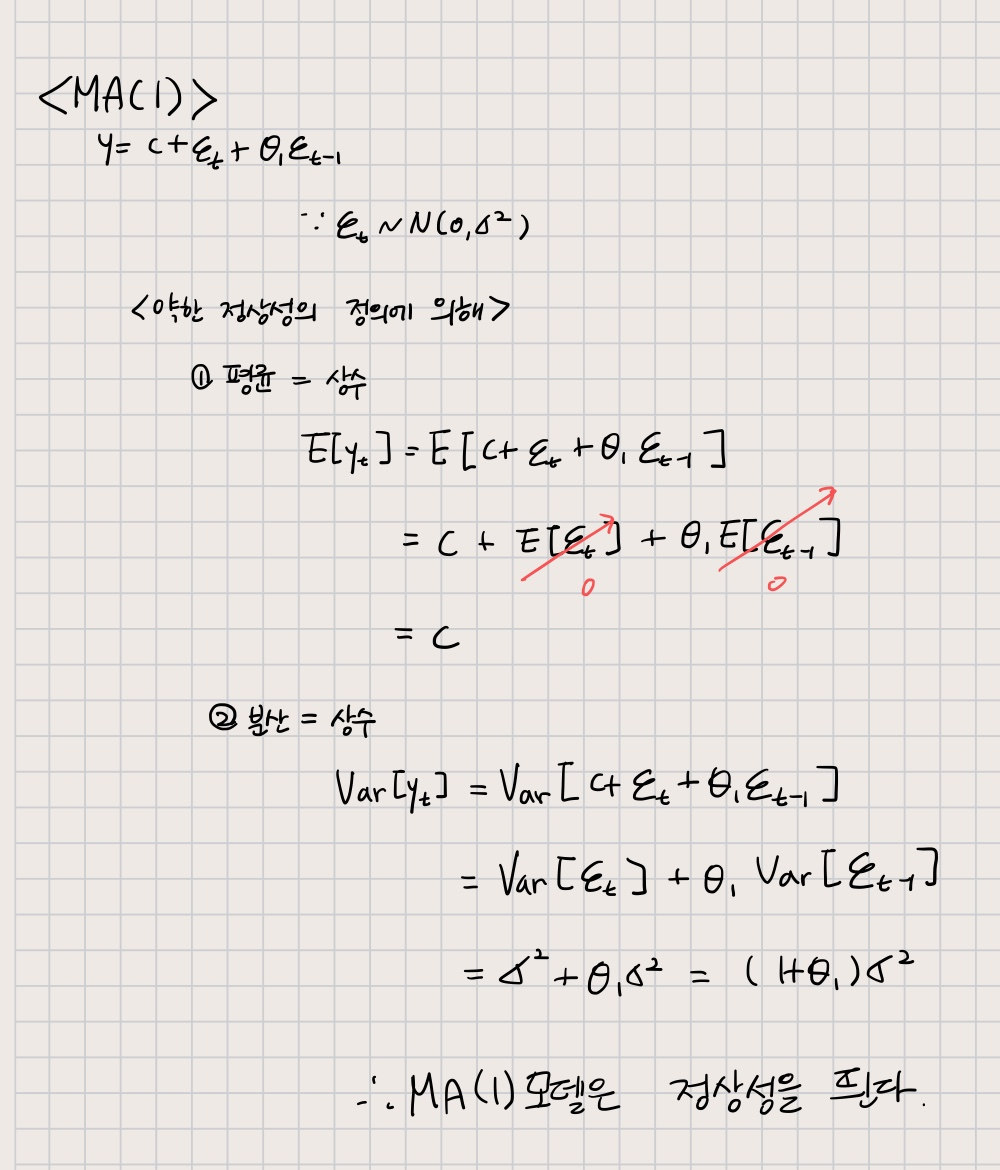
# REF

https://assaeunji.github.io/statistics/2021-08-23-arima/

시계열 분석 시리즈 (2): AR / MA / ARIMA 모형, 어디까지 파봤니?

https://blog.naver.com/PostView.naver?blogId=tjgml1343&logNo=222077619748&redirect=Dlog&widgetTypeCall=true&topReferer=https%3A%2F%2Fwww.google.com%2F&directAccess=false 

[ADsP] 시계열 분석 모델을 공부했다. (AR, MA, ARIMA, ACF, PACF)