4.3 마르코브 보상 프로세스 : 강화학습의 수학적 기초와 알고리즘의 이해

마르코브 보상 프로세스

마르코브 프로세스에 보상 개념을 도입한 것이다.

• 보상은 특정상태에 제공하는 인센티브로 볼 수 있다.
• 누적보상(리턴)에 대한 기대치 계산이 가능하다.

 

< 구성요소 >

➢ $S$ = 상태집합

➢ $P$ = 상태전이확률 $P[S_{t+1} = s^\prime | S_t = s]$

➢ $R$ = 보상(Reward)함수 $R_s = E[R_t | S_t = s]$

➢ $\gamma$ = 감가율(discounting factor)

➢ 에피소드(episode)

ㅤㅤ특정 상태로부터 시작하여 종료 상태까지의 상태-보상 sequence

➢ $G_t$ = 리턴(Return)

ㅤㅤt번째 시각 이후의 (감가율이 반영된) 누적 보상

ㅤㅤ에피소드에서 방문했던 상태별로 얻은 보상의 합

$$ \begin{matrix} G_t &=& R_t + \gamma R_{t+1} + \gamma ^2 R_{t+1} + \cdots \\ &=& \sum_{k=0}^\infty \gamma^kR_{t+k} \end{matrix} $$

 

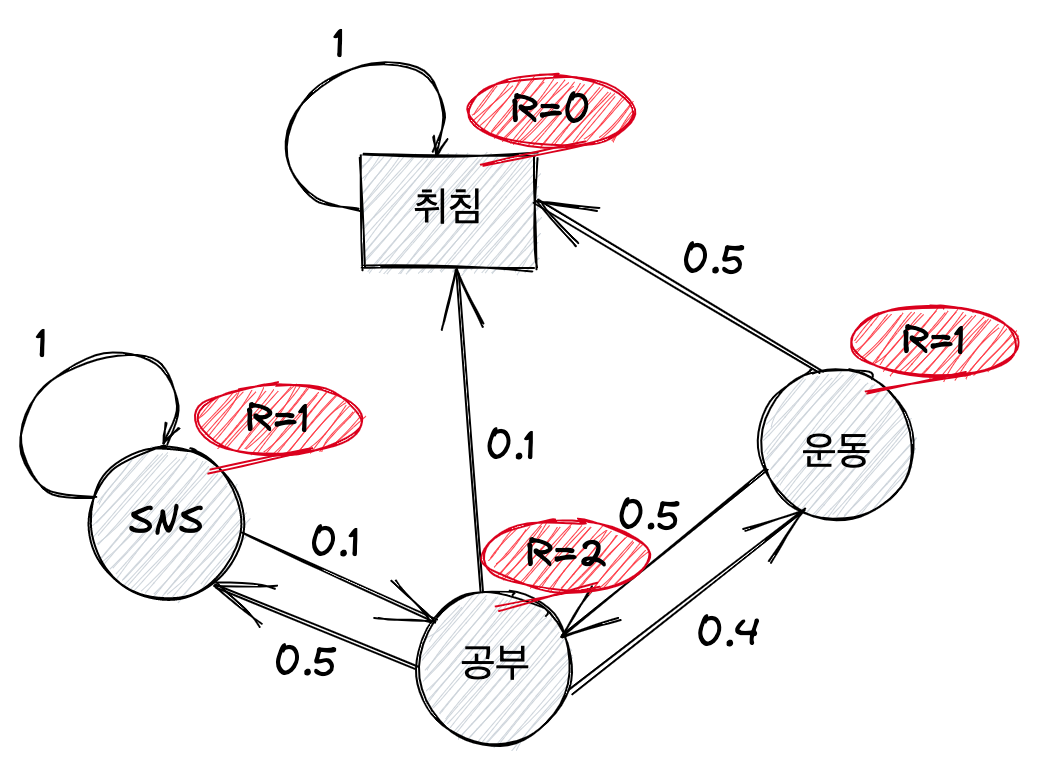
EX)

state transition diagram 과 1 단계 전이행렬

위의 예시로부터 리턴 $G_t$구해보기

• 모든 에피소드가 아니다.
• 에피소드는 또 다른 에피소드의 부분집합일 수 있다.
• 에피소드의 확률을 구할 수 있다.
  • 표의 첫 번째 에피소드의 확률
    = 0.5 x 0.9 x 0.1 x 0.4 x 0.5

 

가치 함수(value function) $V(s)$

→ 어떤 상태가 더 좋고, 나쁜지 평가할 수 있는 지표 필요

→ 프로세스가 진행됨에 있어, 상태 s가 보상측면에서 얼마나 좋은 상태인지 평가하기 위한 지표

→ 특정 상태에서의 리턴(특정 상태로 부터 시작한 에피소드에서 감가율이 반영된 누적 보상)의 기대값

→ 상태 S로 부터 시작하는 프로세스로 부터 기대할 수 있는 누적보상의 평균

1. 모든 에피소드 나열
2. 에피소드 별 발생확률 계산
3. 에피소드 별 누적 보상 합 계산  $v(s) = E [G_t | S_t = s]$

재귀식을 활용한 가치함수 계산

- 해당 상태에서의 보상과 다음 상태에서의 가치들의 가중 합 고려해야 한다.

- 전이 확률이 반영된 다음 상태에서의 가치 값과 연관성 가진다.

가치함수 계산 식 유도

$$ R_s + \gamma \Sigma {s^\prime \in S}P[S{t+1} = s^\prime | S_t = s]V(s^\prime) $$

 

위의 식을 활용하여 아까의 예시에 대입해 보면,

다음과 같이 가치 함수 식을 쓸 수 있음

 

 

가치 함수식을 벡터화 하면,

위와 같이 정리된다. 

 

식 만을 가져와 다시 정리해 보면,

 

$V = R + \gamma PV$ 로 정리가 된다.

우리가 알고 싶은 값은 벡터 $V$이기 때문에 $V$에 대해 묶어 정리하면,

$IV = R + \gamma PV$

$(I - \gamma P) V = R$이 된다.

이 때, $(I - \gamma P)$는 상태전이행렬로 정방행렬이므로 항상 역행렬이 존재한다.

 

따라서,

굳이 모든 상태 별로 에피소드를 나열할 필요 없이 $(I - \gamma P)$의 역행렬을 $R$벡터에 곱하면

각 상태의 가치 값,

어떤 특정 상태로부터 마르코브 체인에 따라 진행되었을 때 각 에피소드의 누적 보상합의 기대치를 계산할 수 있다.