정책 그래디언트의 목표
- 정책을 파라미터화
- 누적보상을 파라미터화 된 정책으로 기술 -> 누적 보상과 정책 파라미터 간의 함수 관계 구축
- 최적화 방법을 통해 누적 보상 관계 함수 최대화
목적함수
반환값의 기댓값으로 이루어진 목적함수 $J$를 최대로 만드는 정책 $\pi(u_t|x_t)$을 구하는 것
- 정책 신경망(policy neural network)
- 신경망(neural network)으로 파라미터화한 정책
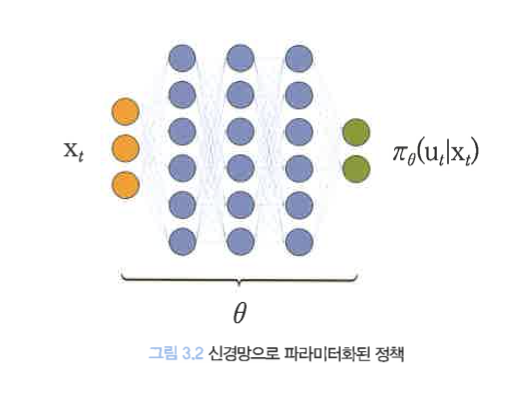
정책이 $\theta$로 파라미터화 됐다면, $\pi_\theta(u_t|x_t)$로 표기할 수 있다.
목적함수 $J$를 최대로 만드는 정책 파라미터 $\theta^*$를 계산하는 것
$$ \begin{matrix} \theta^* &=& argmax J(\theta)\\ J(\theta) &=& \mathbb{E}{r\sim p\theta(\tau)} \left[ \sum\limits_{t=0}^\tau \gamma^t r(x_t,u_t)\right] \end{matrix} $$
- $r(x_t,u_t)$ : 시간스텝 t일 때 상태변수 x_t에서 행동 u_t를 사용했을 떄 에이전트가 받는 보상
- $\gamma \in [0,1]$ : 감가율(discount factor)
- $p_\theta(\tau)$ :
- 기댓값 계산 시, 사용하는 확률밀도함수
- 정책 $\pi_\theta$로 생성되는 궤적의 확률밀도함수
- $\tau$

그러므로, 위의 목적함수 $J$를 다시 전개해보면,
$$ \begin{matrix} J(\theta) &=& \mathbb{E}{r\sim p\theta(\tau)} \left[ \sum\limits_{t=0}^\tau \gamma^t r(x_t,u_t)\right]\\ &=& \int_\tau p_\theta(\tau)(\sum\limits_{t=0}^T \gamma^t r(x_t, u_t))d\tau \end{matrix} $$
확률의 연쇄법칙에 의해
$$ \begin{matrix} p_\theta(\tau) &=& p_\theta(x_0, \tau_{u_0:u_T}) \\ &=& p(x_0)p_\theta(\tau_{u_0:u_T}|x_0) \end{matrix} $$
라 표현할 수 있고, 이를 위의 식에 대입하면
$$ \begin{matrix} J(\theta) &=& \int_{x_0} \int_{\tau_{u_0:u_T}} p_\theta(x_0, \tau_{u_0:u_T})(\sum\limits_{t=0}^T \gamma^tr(x_t,u_t))d\tau_{u_0:u_T}dx_0 \\ &=& \int_{x_0} \int_{\tau_{u_0:u_T}} p(x_0)p_\theta(\tau_{u_0:u_T}|x_0)(\sum\limits_{t=0}^T \gamma^t r(x_t, u_t))d\tau_{u_0:u_T}dx_0 \\ &=& \int_{x_0} \left[ \int_{\tau_{u_0:u_T}} p_\theta(\tau_{u_0:u_T}|x_0)(\sum\limits_{t=0}^T \gamma^t r(x_t, u_t))d\tau_{u_0:u_T}\right]p(x_0)dx_0 \end{matrix} $$
위 식의 대괄호 항은 상태가치 함수 $V^{\pi_\theta}(x_0)$이므로 목적함수는 초기 상태변수 $x_0$에 대한 상태가치의 평균값이 된다.
'Data Science > Reinforcement' 카테고리의 다른 글
| A2C의 어드밴티지 함수 (0) | 2023.06.20 |
|---|---|
| A2C의 배경과 그래디언트의 재구성 (0) | 2023.06.13 |
| 강화학습의 개념 (0) | 2023.05.09 |
| 4.3 마르코브 보상 프로세스 : 강화학습의 수학적 기초와 알고리즘의 이해 (0) | 2022.11.07 |
| 4.1 마르코브 프로세스 개요 : 강화학습의 수학적 기초와 알고리즘의 이해 (2) | 2022.11.02 |




댓글